机器学习 10：激活函数大全

线性激活函数

$$f(x)=ax\\f(x)\in(-\infty,\infty)$$

Sigmoid 函数

$$\sigma(x)=\frac1{1+e^{-x}}$$

优点：

• 对神经元的输出进行归一化
• 用于将预测概率作为输出的模型
• 梯度平滑
• 明确的预测，输出非常接近 1 或 0

缺点：

• 倾向于梯度消失
• 输出不是以 0 为中心，会降低权重更新效率
• 指数运算速度慢

LogSigmoid

$$f(x)=\log(\frac1{1+e^{-x}})$$

Swish

$$f(x)=x*sigmoid(x)=\frac x{1+e^{-x}}$$

Swish 的设计受到了 LSTM 和高速网络中 gating 的 sigmoid 函数使用的启发。我们使用相同的 gating 值来简化 gating 机制，这称为 self-gating。

self-gating 的优点在于它只需要简单的标量输入，而普通的 gating 则需要多个标量输入。这使得诸如 Swish 之类的 self-gated激活函数能够轻松替换以单个标量为输入的激活函数（例如 ReLU），而无需更改隐藏容量或参数数量。

优点：

• 无界性有助于防止训练期间，梯度逐渐接近 0 并导致饱和（有界性也是有优势的，因为有界激活函数可以具有很强的正则化，并且较大的负输入问题也能解决）
• 导数恒 $>0$
• 平滑度在优化和泛化中起了重要作用。

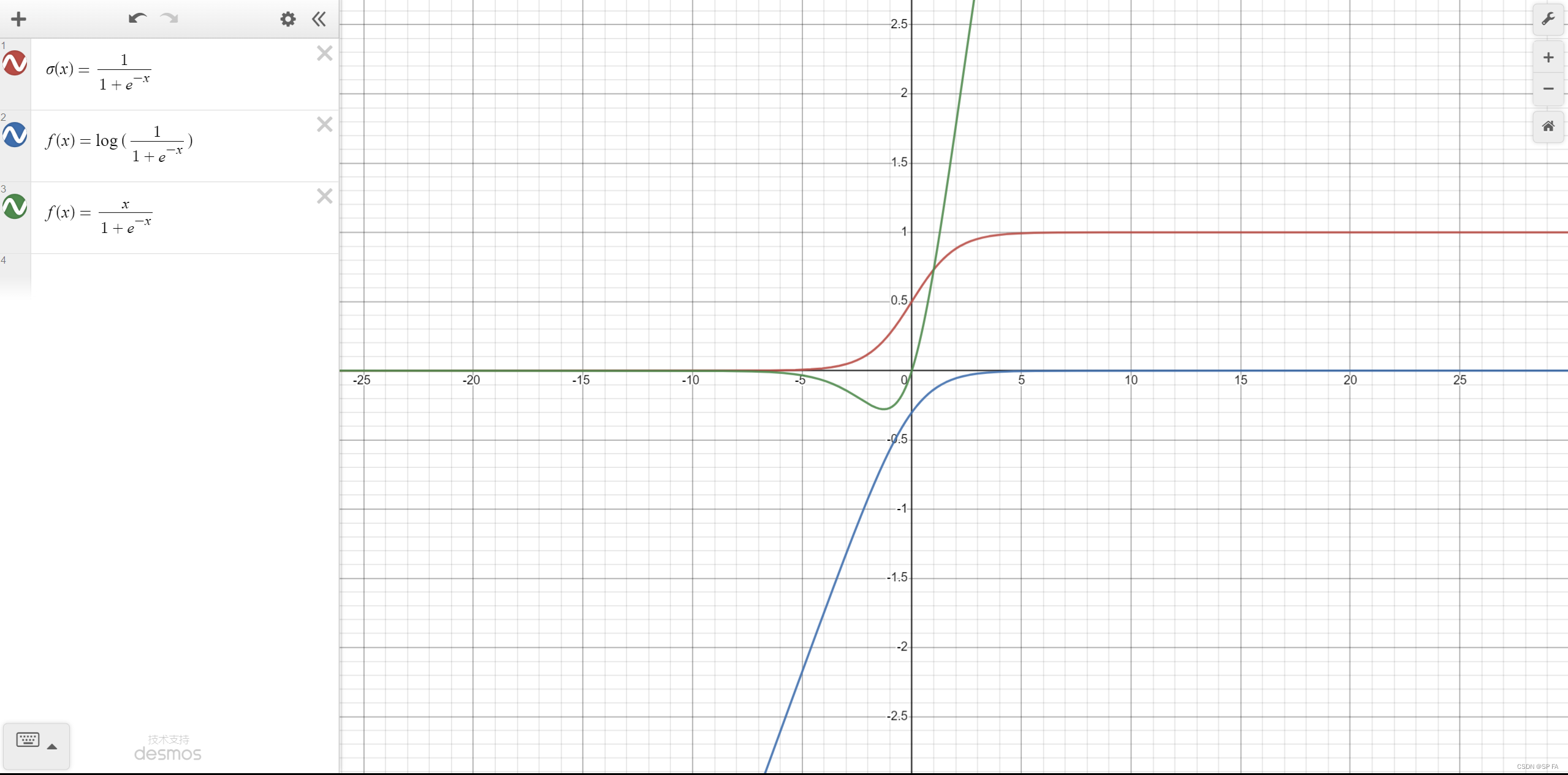
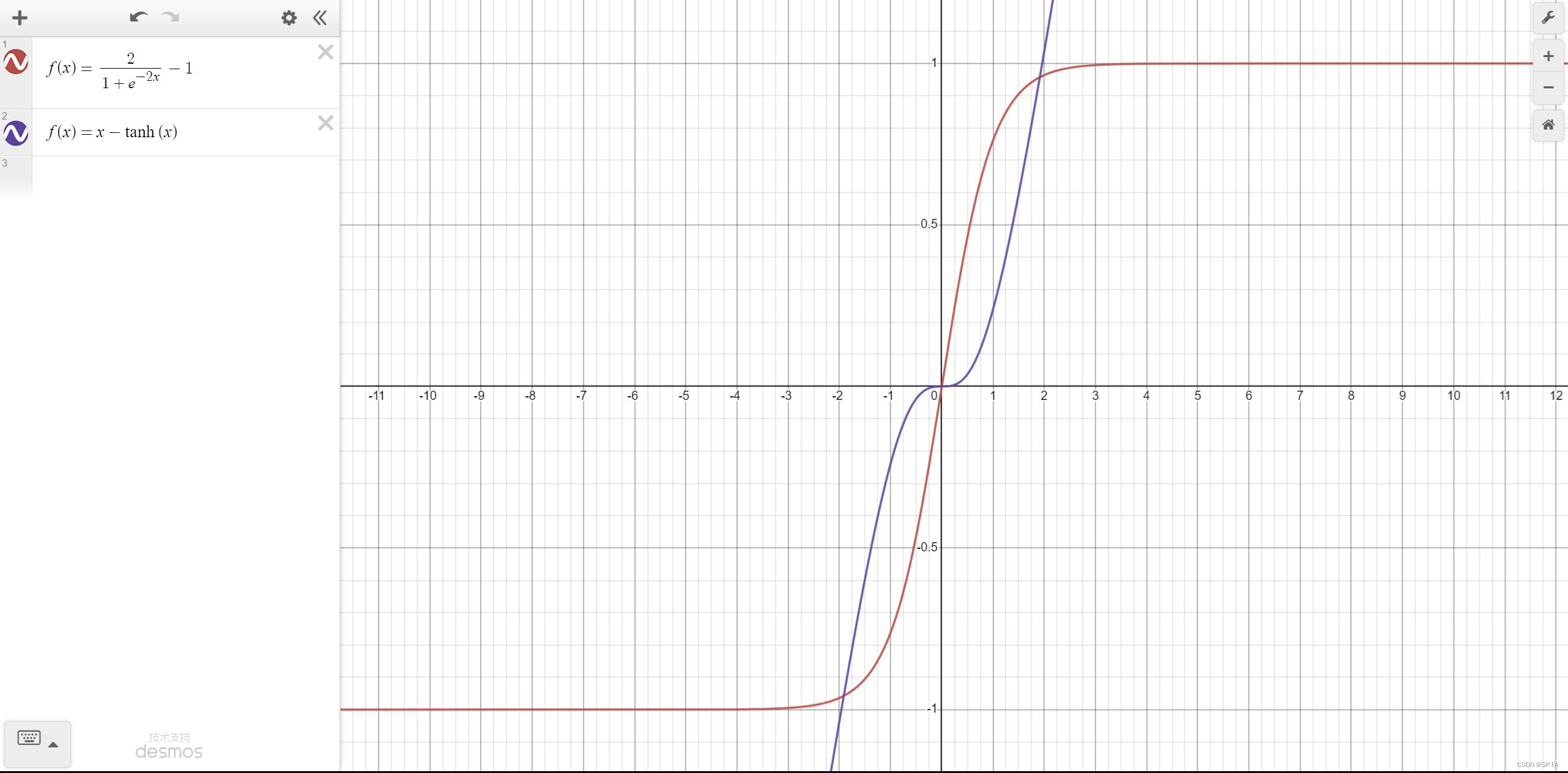
Tanh / 双曲正切激活函数

$$f(x)=tanh(x)=\frac2{1+e^{-2x}}-1$$

与 sigmoid 相比，它的优点就是以 0 为中心，收敛速度比 Sigmoid 快

一般在二分类问题中，tanh 用于隐藏层，而 sigmoid 用于输出层

TanhShrink

$$f(x)=x-tanh(x)$$

Softsign

$$f(x)=\frac x{1+|x|}$$

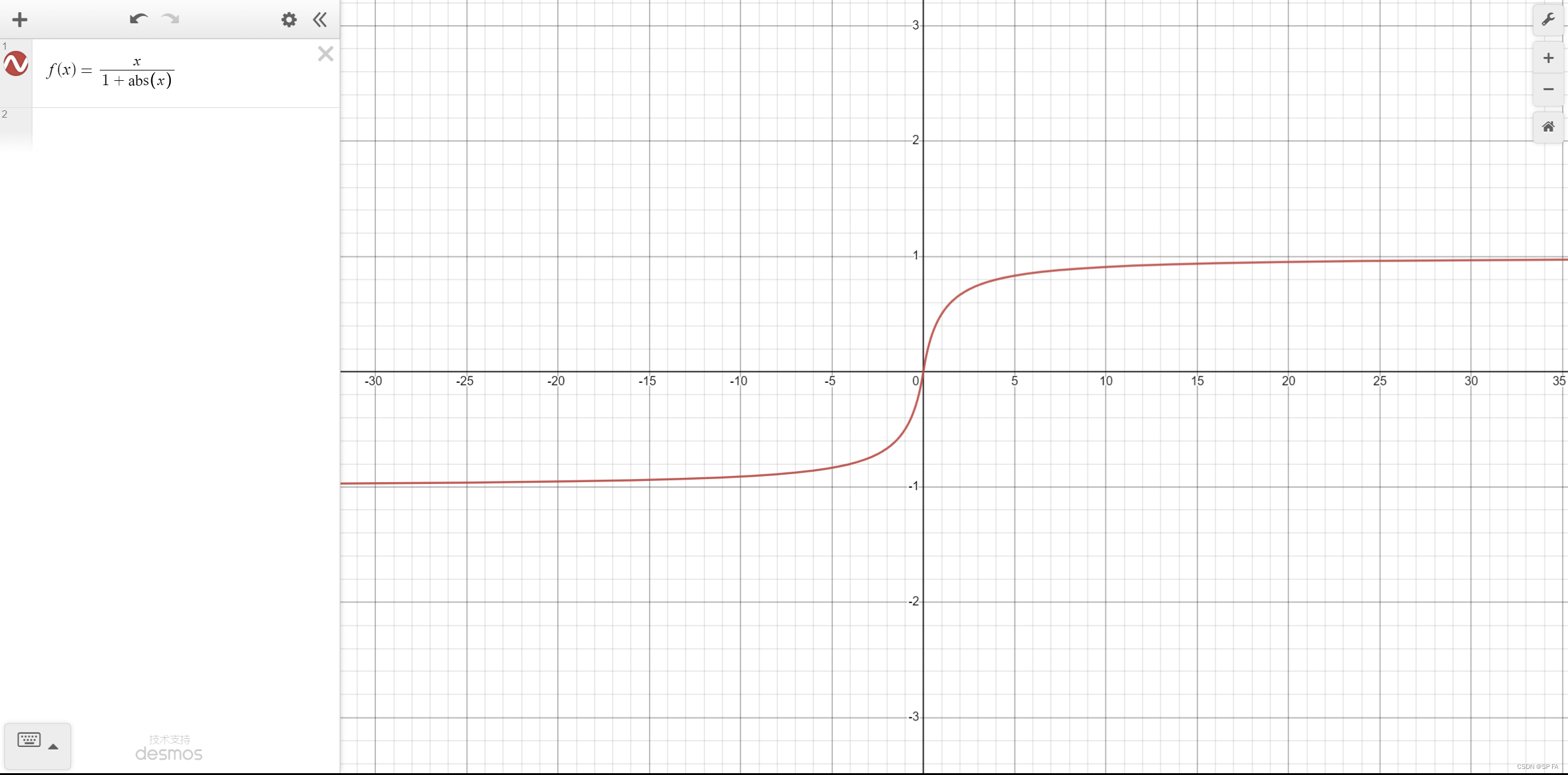
Softsign 是 tanh 的一个替代选择，相比于tanh，Sotsign 的曲线更平坦，导数下降的更慢一点，这使得它可以缓解梯度消失问题，可以更高效的学习。

ReLU 函数

$$\sigma(x)=\max(0,x)$$

优点：

• 当输入为正时，不存在梯度饱和问题
• 计算速度快

缺点：

• Dead ReLU 问题，当输入为负时 ReLU 失效。在正向传播过程中有些区域会很敏感，有些不敏感。但是在反向传播过程中，如果输入负数，则梯度完全为 0。

梯度饱和：

有些函数（如 Sigmoid 或 Tanh）自变量进入某个区间后，梯度会非常小，函数曲线越来越趋近一条水平直线。梯度饱和会导致训练过程中梯度变化缓慢，从而造成模型训练缓慢。梯度饱和是造成梯度消失的原因之一。

BReLU

限制 ReLU 的输出不超过 $n$。$f(x)=\min(\max(0,x),n)$

Leaky ReLU

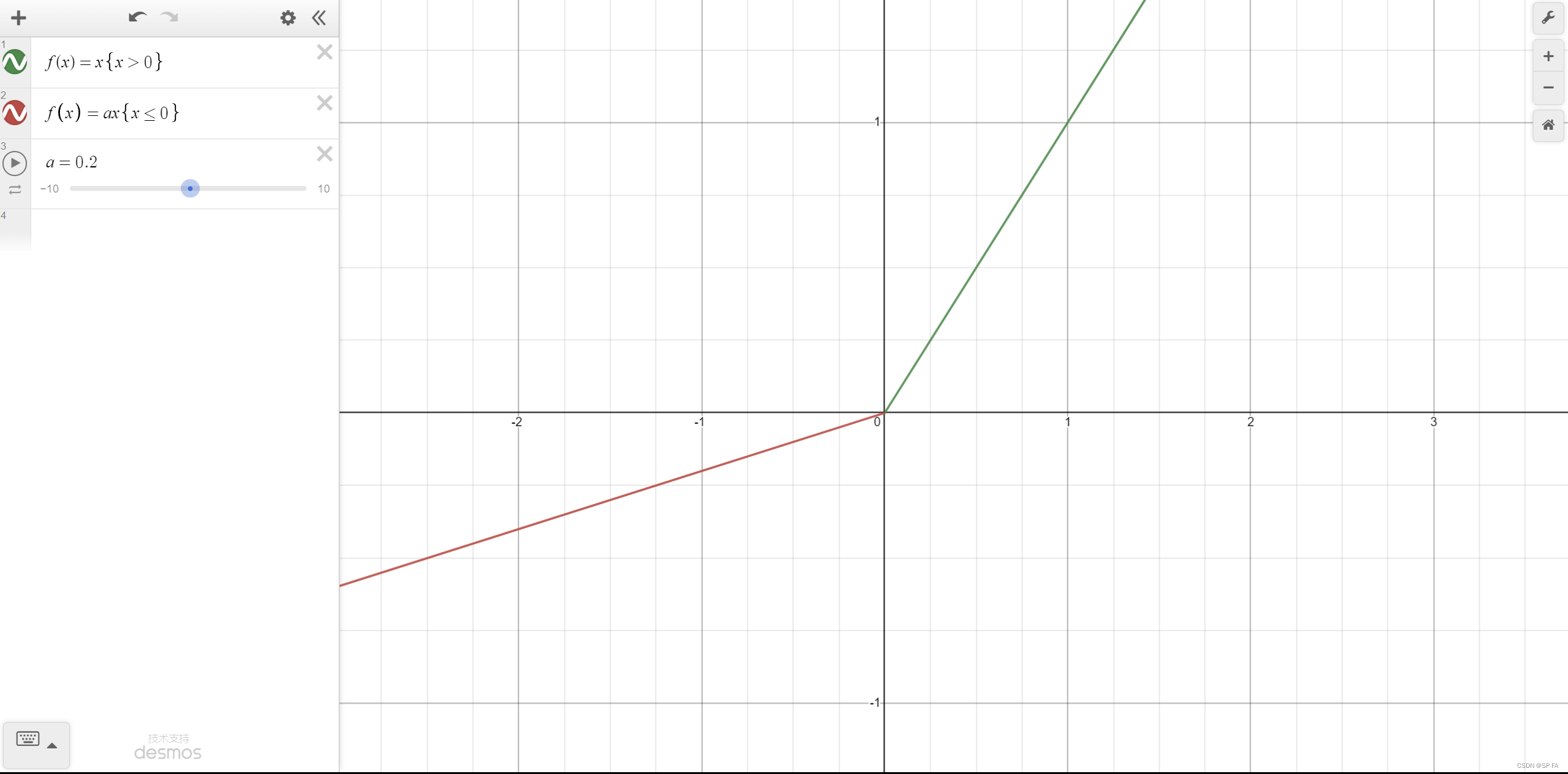
一种专门设计用于解决 Dead ReLU 问题的激活函数$f(x)=\begin{cases}x&x>=0\\ax&x<0\end{cases}$其中 $a$ 值很小，一般在 0.01 左右。

注意： 从理论上来讲，Leaky ReLU 具有 ReLU 的所有优点，且不会有 Dead ReLU 问题，但在实际使用中，没有完全证明 Leaky ReLU 总是比 ReLU 好。

PReLU

和 Leaky ReLU 很像，唯一的不同是函数中的 $a$ 是一个可通过反向传播学习的参数。

RReLU

对 Leaky ReLU 的另一种改进。在训练时，$a$ 是给定范围内取样的随机变量，而测试时 $a$ 变为固定值。这里 $a$ 服从均匀分布。

ELU

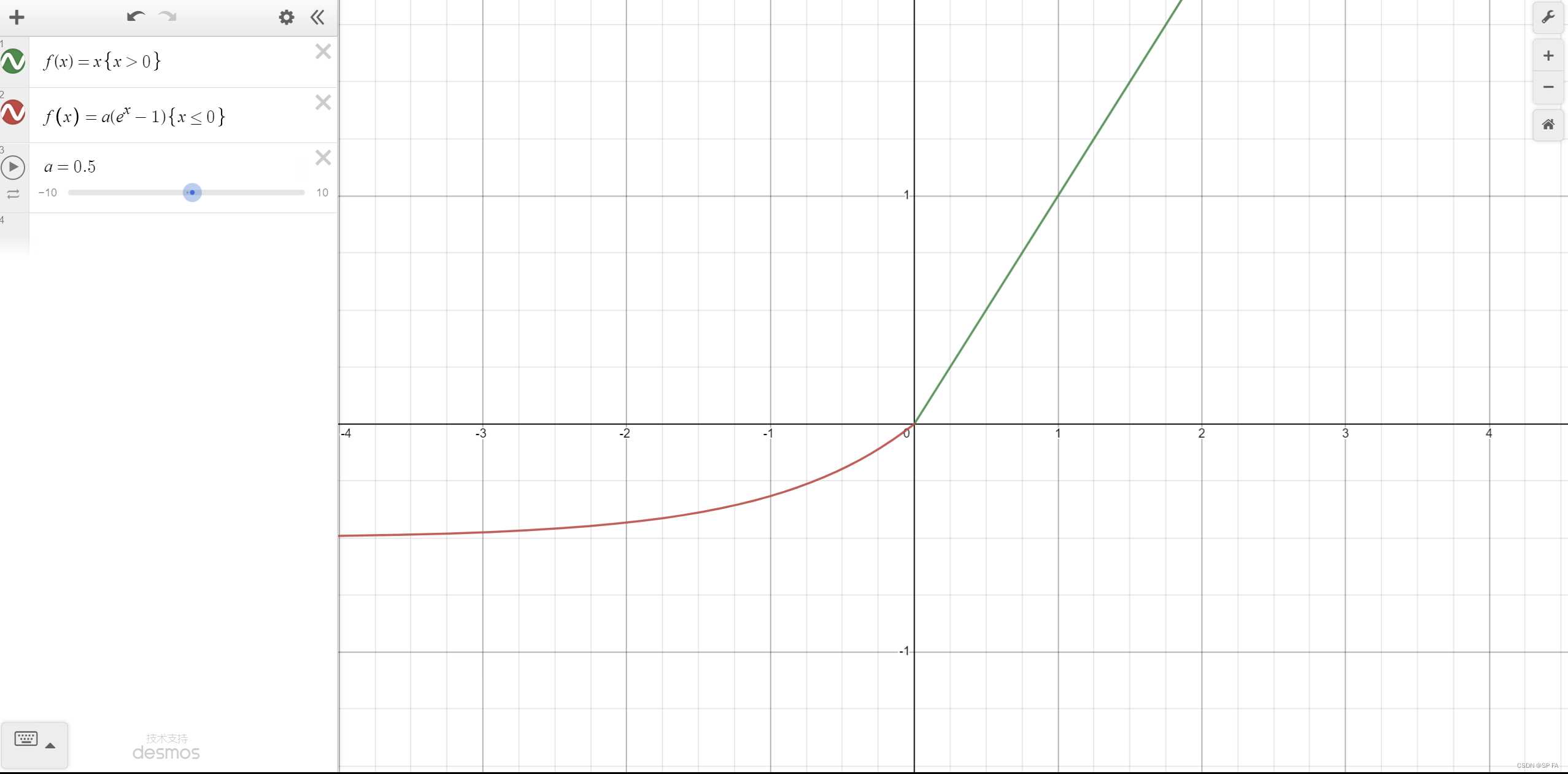
ELU 的提出也解决了 ReLU 的一些问题。$g(x)=\begin{cases}x&x>=0\\a(e^x-1)&x<0\end{cases}$优点：

• ReLU 的所有优点
• 没有 Dead ReLU
• 与 ReLU 相比，ELU 有负值，这会使激活的平均值接近零。均值激活接近于零可以使学习更快，因为它们使梯度更接近自然梯度。
• 在较小的输入下会饱和至负值，从而减少前向传播的变异和信息。

缺点：

• 有指数运算，计算强度更高
• 从理论上来讲，ELU 具有 ReLU 的所有优点，但在实际使用中，没有完全证明 ELU 总是比 ReLU 好。

SELU

SELU和ELU的形式比较类似，但是多出一个 scale。$g(x)=scale*\begin{cases}x&x>=0\\a(e^x-1)&x<0\end{cases}$优点：

• 能够对神经网络进行自归一化

CELU

$$g(x)=\begin{cases}x&x>=0\\a(e^\frac xa-1)&x<0\end{cases}$$

GELU

$$f(x)=\frac12x(1+\tanh(\sqrt{\frac2\pi}(x+0.044715x^3)))$$

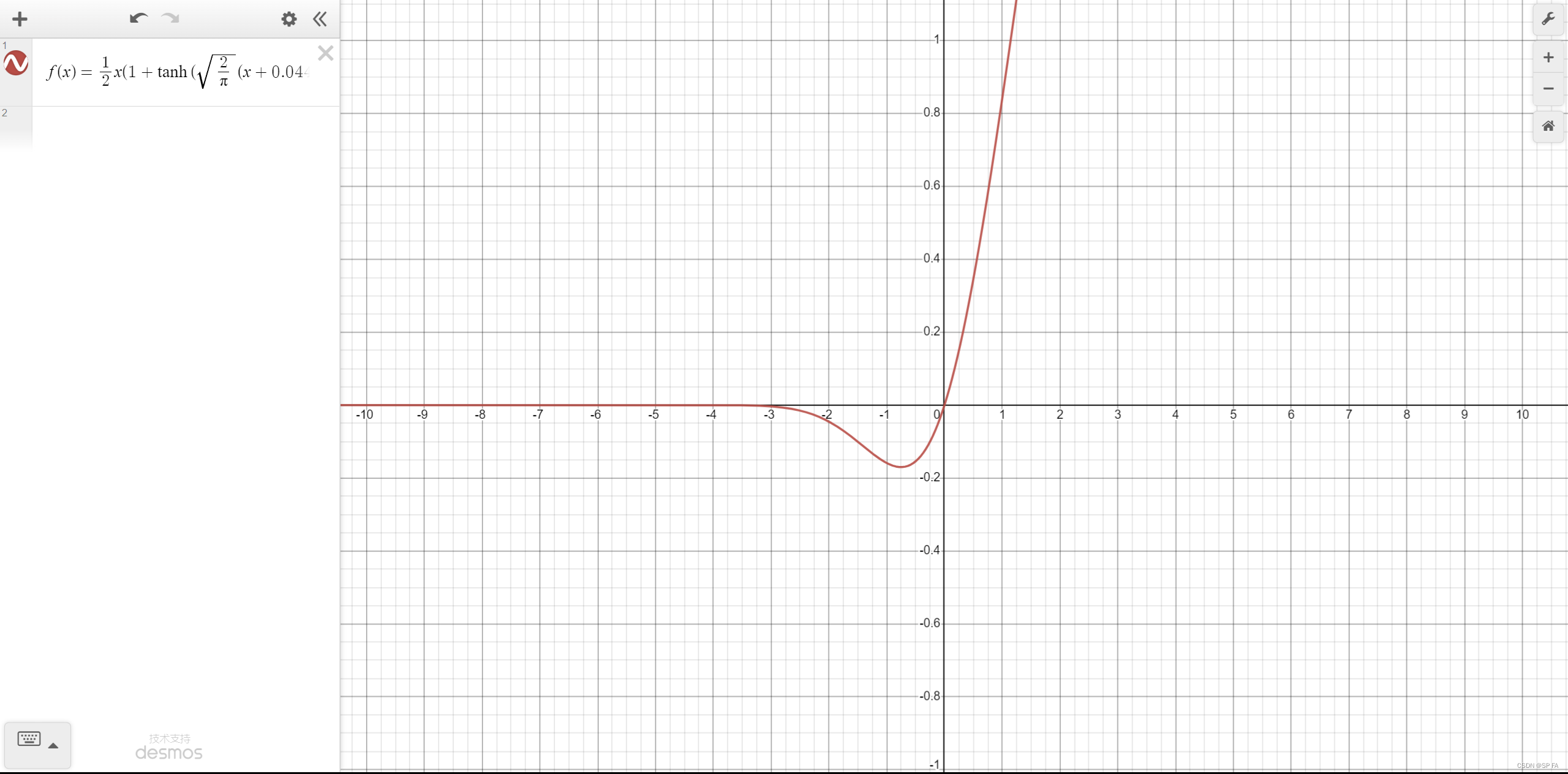
GELU 函数结合了 ReLU、Dropout、Zoneout 的思想，并且加入了正态分布的方法。

• ReLU: 输入大于 0 则输出，否则不输出。
• Dropout：随机决定是否输出。
• Zoneout：Dropout 的一个变种，在时间维度上随机决定是否输出，或者可以理解为是否跳过这一步直接到达下一步。

这三者的相同点总结为一句话，就是通过对输入乘上 1 或 0 来控制神经元是否输出。而 GELU 也采用了这个思想，但它是否输出是由自身分布情况决定的，更具体一点，由输入项有多大概率大于其它输入而决定。

更具体一点：
将输入 $x$ 乘以一个服从伯努利分布的数 $m$，而该伯努利分布由依赖于 $x$

$$m\sim\text{Bernoulli}(\Phi(x))\\~\text{where }\Phi(x)=P(X\le x)$$

由于神经元的输入往往遵循正态分布（尤其是深度网络中普遍存在 Batch Normalization 的情况下），所以公式中 $X$ 表示其它输入，服从标准正态分布 $X\sim N(0,1)$，那么 $\Phi(x)$ 就表示标准正态分布的累计分布函数。此时 GELU 函数可以写成：

$$\text{GELU}(x)=x\Phi(x)+0*x(1-\Phi(x))=x\Phi(x)$$

另外累积分布函数 $\Phi(x)$ 可以用误差函数表示：

$$\Phi(x)=\frac12[1+\text{erf}(\frac x{\sqrt2})]$$

而误差函数是一个非初等函数，所以我们又需要用一个初等函数 tanh 去拟合，最终就有了上面 GELU 的公式。

优点：

• 似乎是 NLP 领域的当前最佳，尤其在 Transformer 模型中表现最好
• 能避免梯度消失问题

Softmax 函数

用于多分类问题的激活函数，在多类分类问题中，超过两个类标签则需要类成员关系。对于长度为 $K$ 的任意实向量，Softmax 可以将其压缩为长度为 $K$，值在 $(0,1)$ 范围内，并且向量中元素值的总和为 1 的实向量。

$$Softmax(\vec z)=\frac{e^{z_i}}{\sum^K_{j=1}e^{z_j}}$$

Softmax 与正常的 max 函数不同，max 函数仅输出最大值，但 Softmax 会确保较小的值具有较小的概率，并不会直接丢弃。可以认为它是 argmax 函数的概率版本。

缺点：

• 在 0 点不可微
• 负输入的梯度为零，这意味着对于该区域，权重不会在反向传播期间更新，因此会产生永不激活的死亡神经元。

Maxout 函数

$$f(x)=\max(w_1^Tx+b_1,w_2^Tx+b_2,\cdots,w_n^Tx+b_n)$$

可以看出 ReLU 就是它的一个变形。它可以近似任何一个连续函数。只有 2 个 maxout 节点的多层感知机就可以拟合任意的凸函数。单个 Maxout 节点可以解释为对一个实值函数进行分段线性近似 (PWL) ，其中函数上任意两点之间的线段位于凸函数的上方。

但它增加了参数和计算量。

Softplus 函数

$f(x)=\ln(1+e^x)$类似 ReLU 函数，和 ReLU 一样是单侧抑制，但是相对平滑。

优点：

• 与 ReLU 不同的是，SoftPlus 的导数是连续的、非零的、无处不在的，这一特性可以防止出现 Dead ReLU 现象。

缺点：

• SoftPlus 是不对称的，不以0为中心，存在偏移现象。
• 其导数常常小于1，也可能会出现梯度消失的问题。